In the last lesson, I said that this lesson is the most important lesson of all…

So welcome to risk management or the lesson about how to minimize your trading risks. This is also commonly known as money management.

I already talked a lot about setting stops and that this is a great way to reduce your risk of losing money. It should be an integral part of your trading system by now.

But in all previous examples, I never talked about one of the most important things to ask when buying a stock.

Have you noticed what I left out until now?

It’s the answer to the all-important question: HOW MUCH?

How many stocks to buy from company ABC? Yes, we decided to buy – because of our stock picking system. And yes, we set our stop (or trailing stop) as per our profit taking strategy, as well as to reduce risk.

But… should I buy 10 stocks? Or 100? Or 10,000?

Should it be the same number of stocks for each trade, independent of the share price? Or should the total amount of money spent per trade be the same for each trade?

It turns out… NONE of the above. And I will explain why, and how to decide how many stocks to buy for each trade in this lesson.

But first…

 

My first trade, again… and a coin flip game

I have talked already about one of my first trades – Blackberry stocks were “cheap” and I jumped right in, losing a lot of money.

One big reason for this to happen (apart from all the other silly mistakes I made) was that I did not know how much I should buy.

So, I used my entire portfolio money on that single trade. AND I had no stop price.

In hindsight, I was lucky to get out of that trade losing only $2,000. It could have been easily 10 times more. I chickened out – and believe me, being brave when prices fall is not a good thing when being a trader!

If I had stuck to my guns and kept these stocks, I would have gone bankrupt. So much for buying a “brand”. Just think about the Enron or Worldcom disasters. Or Nokia 🙂

Anyway, why is it so important to know how many stocks to buy?

Because putting a stop is not enough. Putting a stop price limits how much you are willing to risk per share – but not on how much you are willing to risk in total.

By the way… how much could you afford to risk per trade?

 

Let’s play…

Let’s play a simulated trading game.

Imagine each of your trades is like a coin flip. It’s a fair coin, and your chance of winning is 50%.

That does not sound like great odds, but if you remember about expectancy, it’s about how much you win per game, not only how often.

In this case, let’s assume if you win you receive 30% more money than you put on the table.

 

 

If you bet $100, then if you win you will get $130. If you lose, you lose $100.

That’s a game with positive expectancy – on average you should make $15 per game. That’s not bad!

Now if you had a total capital of $1,000 – how much would you bet in each coin flip? $100? Or all in? Or $500?

Assume that you will play 100 times in a row… if you still have the cash to play.

Here is what I want you to do: Make a guess about the chance that you finish the game with more money than when you started.

Is there a 90% chance that you end up with more money? Or is it a 50% chance? Anything goes!

Make your guess.

I run a little simulation that calculates how likely you are to grow your portfolio over 100 coin flips (= trades), depending on how much percent of your capital you risk per flip/trade.

I simulated what would happen if we risk 50%, 25%, 10% or only 1% of the total portfolio money.

 

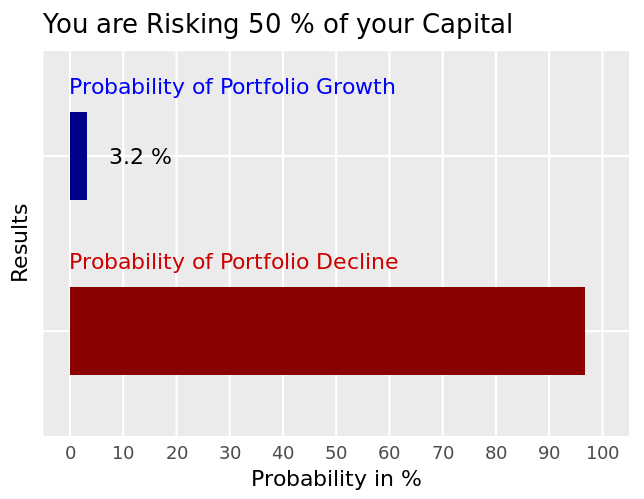
When risking 50%, or $500 out of $1,000, then your odds of increasing your capital are only at around 3%.

Seriously, can you believe that?

By risking half of your capital on every trade, it’s nearly guaranteed that you will lose money in the long run… although it’s a positive expectancy system!

Let’s see if things improve if we dial it down a bit.

 

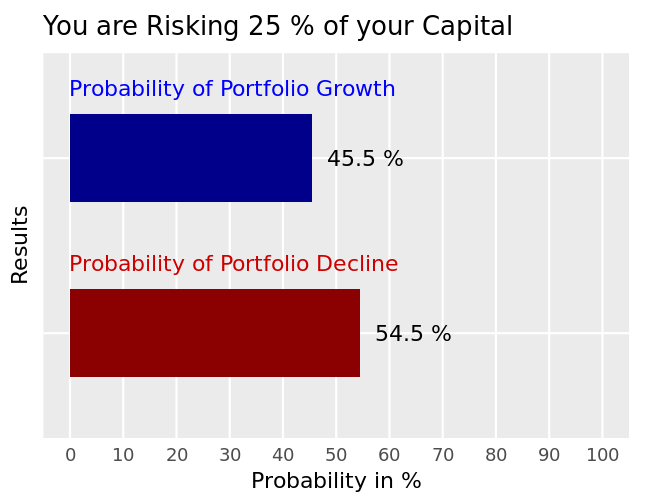
When risking 25%, odds are improving but they are still not great. Our chance to lose money is still above 50%.

 

 

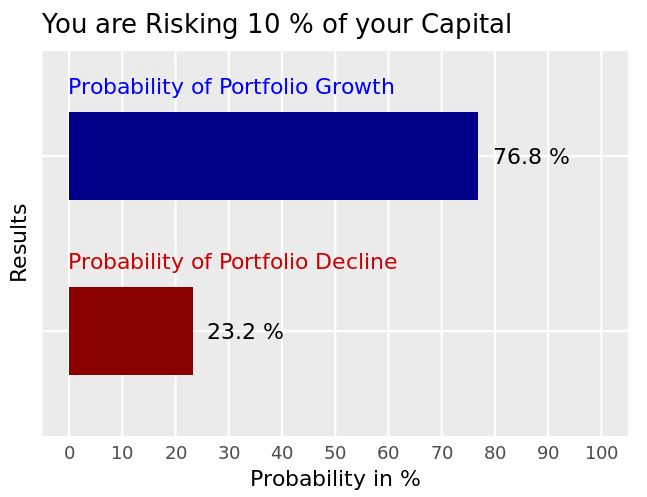
When risking 10% of capital per trade, we are starting to do better.

Now in 3 out of 4 games, we are actually winning money. That’s good. Let’s see what happens if we risk even less: only 1% per flip.

 

 

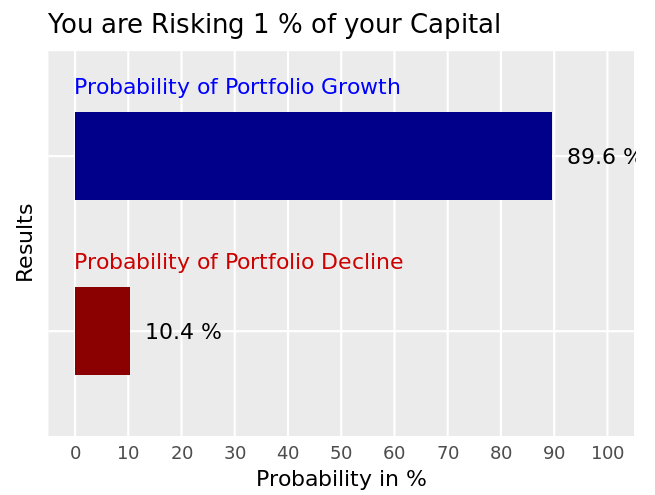
That’s better. Now we make money in 9 out of 10 games.

Still, there is a risk of losing – but that’s what investments are about. You take a (hopefully calculated) risk to increase your wealth.

Just by changing the size of your bet, you reduced your risk of losing money from 97% to 10.4%… that’s a factor of 9!

Remember, nothing else has changed…

The odds are the same, the reward-to-risk ratio is also the same, everything remains the same, except the total amount you put on the table for each bet.

How amazing is that?

 

Now you know… positive expectancy is not enough

It’s just a simple simulation – and I said before, take simulations with a grain of salt.

But it tells a compelling story and explains one of the key reasons why beginner traders fail to make money: They risk too much of their money per trade.

But why is the effect of risking even moderate amounts so devastating?

Take the case of risking 50% of your capital.

If you lose a single trade, then you need to grow your capital by 100% just to break even. If you lose the second trade, you have only 25% of your capital left… and you need to quadruple the amount just to break even.

 

 

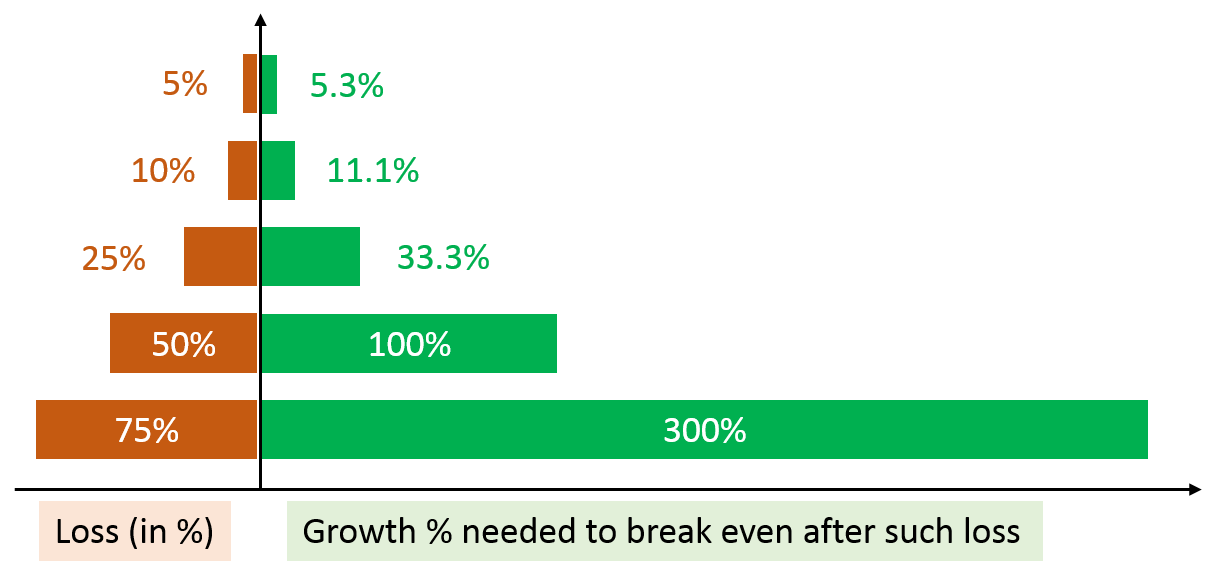
Now think of capital growth rates for savings accounts: 0.5% per year, if you are lucky.

Or the average stock market growth per year, around 8%…

Growing your portfolio by 100% or more just to break even is a killer. It usually does not happen.

Having a series of losing trades is common.

It’s just like with coin flips… random does not mean regular heads or tails. There can be a long series of heads (or tails) before changes happen.

It’s the same in trading. If the market is in a phase that does not favor your type of trading system, then there will be a long series of losses.

That’s normal, and the important thing is to survive this phase so you are ready when a new phase starts… the one where your system makes many winning trades for you.

So, it’s all about preserving your capital during times of bad trades so that you are still in the game when things improve.

What would be acceptable amounts to risk per trade? I suggest no more than 1% or your portfolio value, and preferably less. Myself I usually use 0.25% of capital – a quite low amount. That means if you have a starting capital of $100,000, you would risk $250 per trade.

Expert traders think that risking more than 2% of your capital per trade makes you a gunslinger… and imagine what that means if you lose 20 trades in a row!

 

Measuring performance through risk taking

It’s important to evaluate your system’s performance – so you can understand if it has a positive expectancy.

How to do that?

We know how much we win or lose per trade (if we document it). But it is not very helpful when trying to understand performance.

What we like to know is how well a trade performed compared to the risk that we took.

In the previous lesson, I already used the term “reward-to-risk ratio” a couple of times. And that’s how we can compare trades, even if we risk different amounts for each.

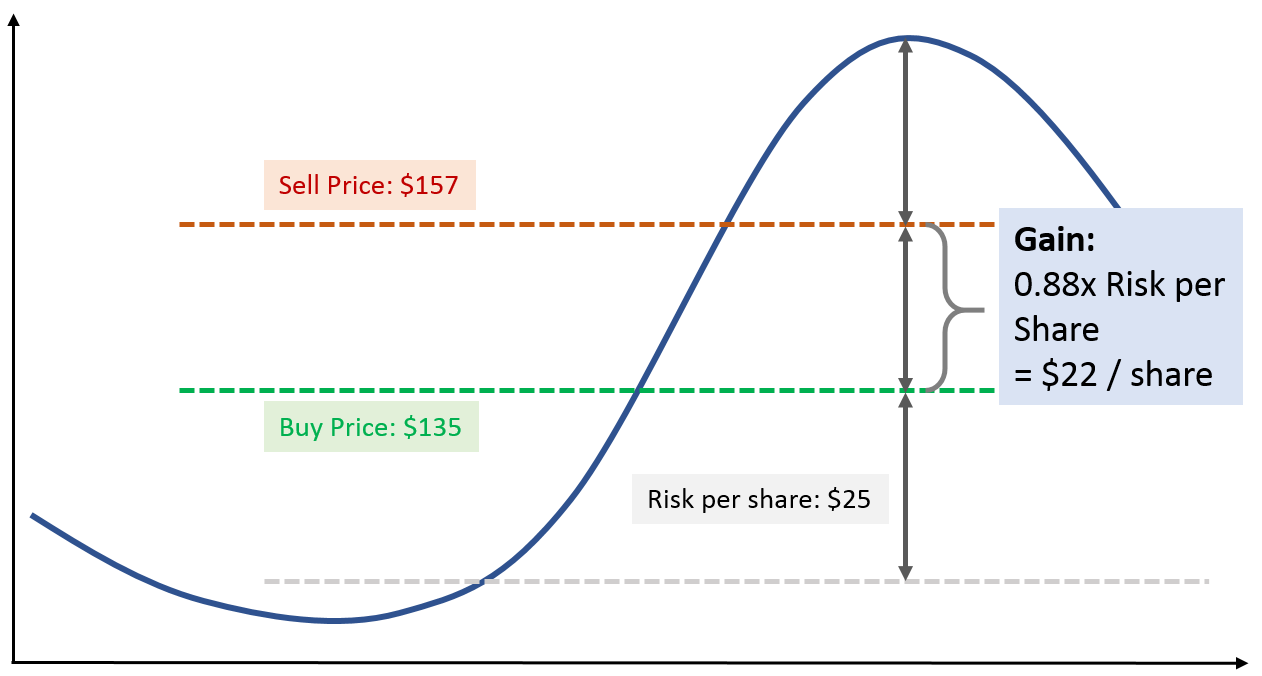
Look at these 2 trades below: which one performed better?

 

 

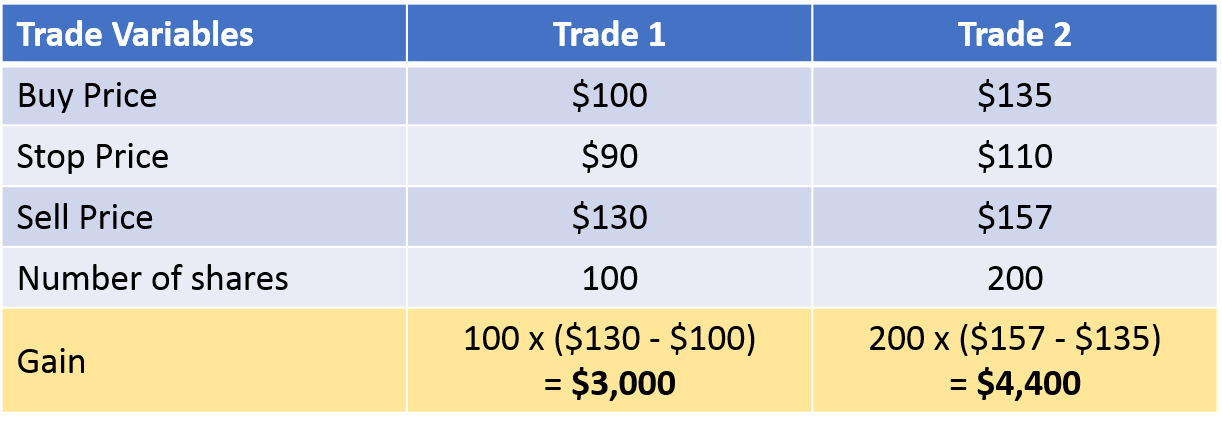
It appears obvious – Trade #2 made more money!

The price moved from $135 to $157, that is less than for Trade #1, from $100 to $130, but we bought more shares. Sounds good, right?

But let’s look at some additional trade variables:

• How much did it cost us to buy these stocks?
• How much money did we risk on each trade (by setting the stop price)?

 

 

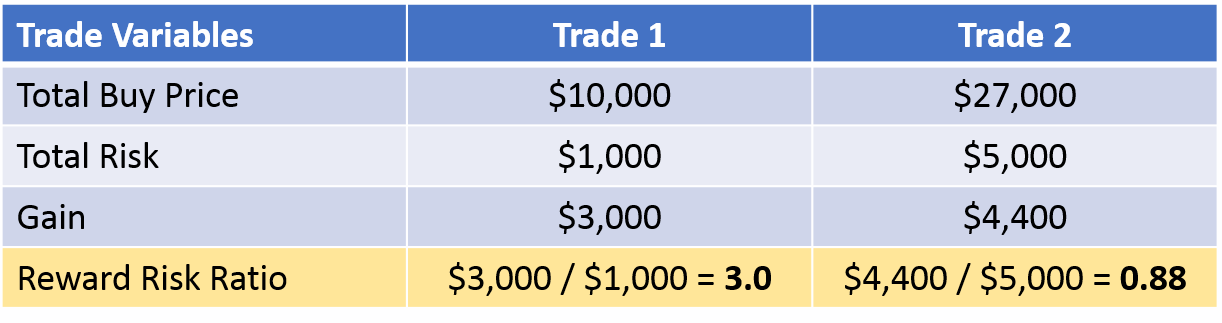
First of all, we spent $27,000 for Trade #2 vs. only $10,000 for Trade #1, that’s more than 2 ½ times the money.

Yet, our gain from Trade #2 was less than 1 ½ times the gain of Trade #1. That’s an indicator that Trade #2 was not as good already.

Now let’s look at the risk per trade (the money you put on the table… your “bet”). How do we calculate it?

Here it goes:

Risk per Trade = Number of Stocks X (Buy Price – Stop Price)

Let’s plug in the numbers:

Trade #1: Trade Risk #1 = 100 x ($100 – $90) = 100 x $10 = $1,000

Trade #2: Trade Risk #2 = 200 x ($135 – $110) = 200 x $25 = $5,000

So, we risked 5 times more money on the second trade than on the first.

Big difference! Now if you calculate the Reward to Risk Ratio for each you will see how poor the second trade performed. We basically gained less than we put at risk.

Imagine all our trades were like this, but our win rate was below 50%… we would go bankrupt!

 

Risk is not how much your stocks cost

Did you notice that we had to spend $10,000 for buying the stocks for Trade #1, but our risk was only $1,000?

• We bought 100 stocks at a price of $100 each -> total spending: $10,000
• But we decided to bail out of the trade if the price goes below $90 per trade
• Means, IF the price hits $90, we would sell 100 stocks at $90 -> giving us back $9,000
• That’s a loss of $1,000, or 10% of what we actually spent

 

 

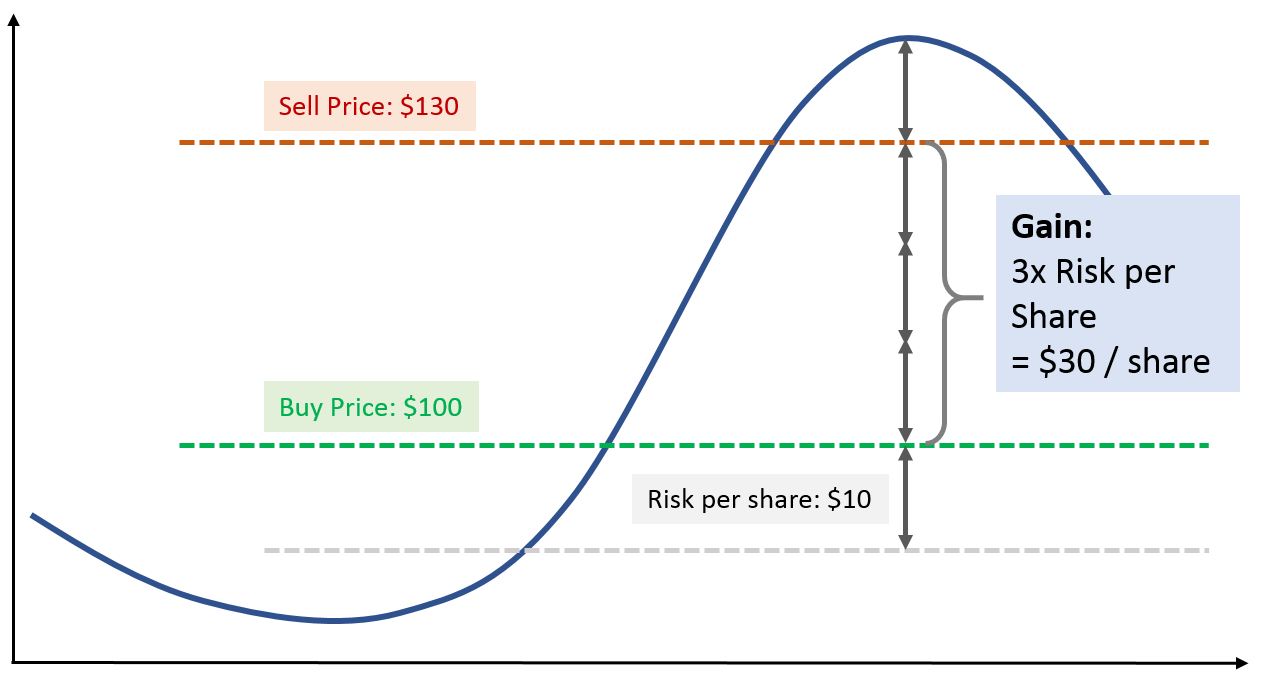
That’s an important concept:

It means that if we know how much money we want to risk per trade, then we can calculate how many stocks we need to buy – and hence how much money we actually spend.

Why is that so important?

Because we want to set a risk limit per trade based on how much capital we have available.

 

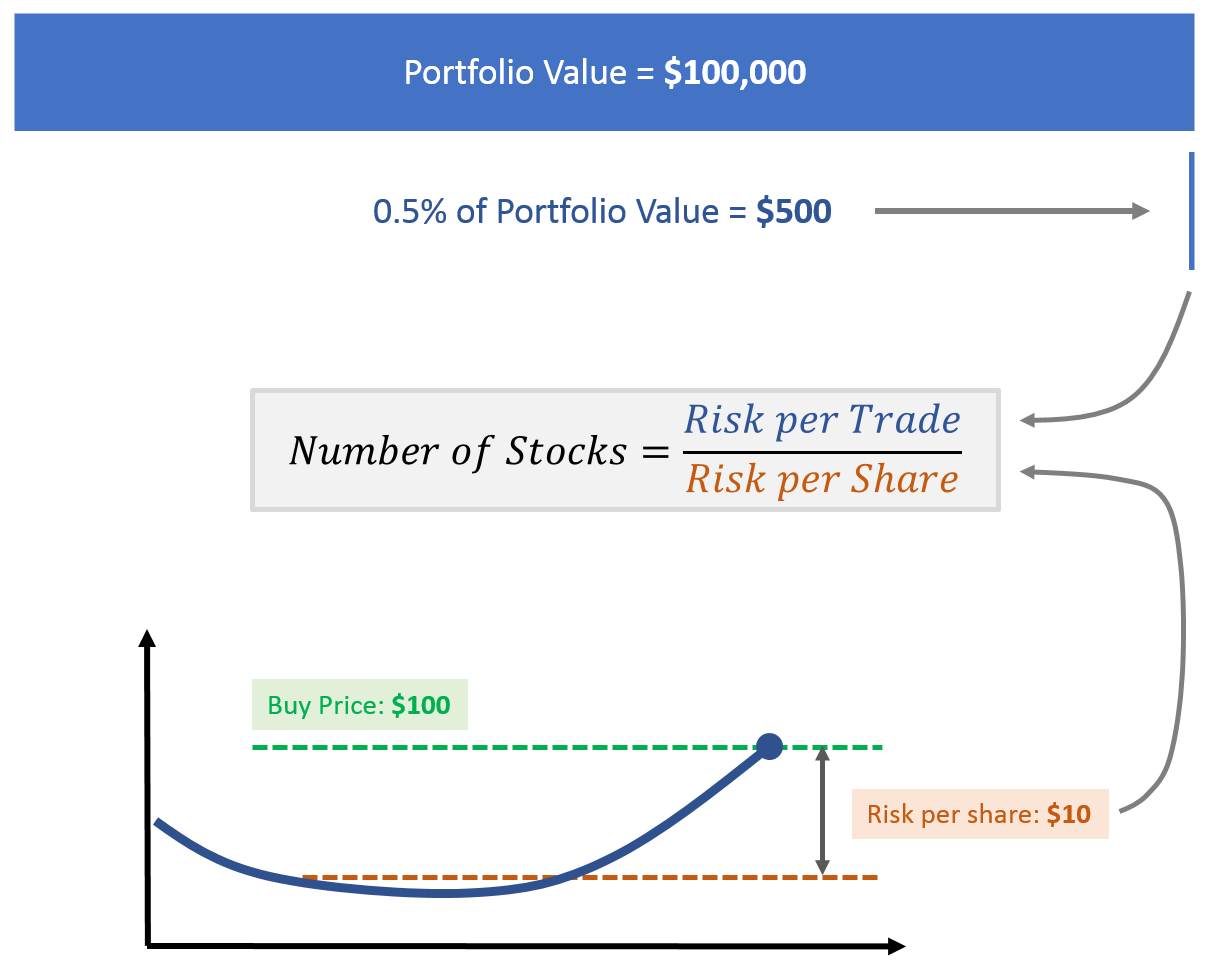
Let’s go through an example with these inputs:

• Our capital is $100,000
• We accept to put 0.5% of capital at risk for a single trade, means $500 for now
• We picked a stock from our stock picking system with a buy price of $100
• We decided upon the initial stop price at $90, or 10% below the buy price

How many stocks should we buy and how much would it cost us?

 

Here we go:

• We know that we will risk $500 for this trade
• We know the maximum risk per share from the stop and buy price: $10
• Therefore, we can buy $500 / $10 = 50 stocks
• Buying 50 stocks at $100 each will cost us $5,000 (plus fees)

 

 

With the capital available, we could maintain 20 such trades at the same time (actually a bit less because of commission costs – but that’s not the point here).

Let’s do another example: this time with Trade #2.

How many stocks should we have bought and what would it have cost us, assuming buy price and stop price stayed as per example and with the same risk settings as before?

• Buy price: $135
• Stop Price: $110, a maximum risk of $25 per share
• Maximum risk: $500
• Number of stocks = $500 / $25 = 20 stocks
• Buying 20 stocks at $135 each will cost us $2,700

 

 

What happens if our capital changes?

Over time and more and more trades, our amount of capital will change, either upwards or downwards. And so will the risk we are taking.

Example: our capital increased to $104,000 after several trades. How will this change our single trades?

Using the example of Trade #1:

• Risk per trade = capital X risk percentage = $104,000 x 0.5% = $520
• Buy price: $100, Stop Price: $90, maximum risk per share = $10
• Number of stocks = $520 / $10 = 52 stocks
• Buying 52 stocks at $100 each will cost us $5,200.

So, with more capital, we will buy more stocks, but the risk per trade, in relation to capital remains the same.

If our capital decreases, the risk per trade decreases accordingly (in absolute terms).

 

How will things look after 100 trades?

We will look at a simplified system that has the following characteristics:

 

 

If we break this down to 100 trades, then, on average, we will have:

• 10 trades that lost as much as we risked per trade
• 50 trades that lost half of what we risked per trade
• 35 trades that won as much as we risked per trade
• 5 trades that won 6 times as much as we risked per trade

Is this a system with positive or negative expectancy? After all, 60 out of 100 trades are losing trades.

Expectancy = 10 x (-1) + 50 x (-0.5) + 35 x (1) + 5 x (6) = 30

 

Here is how it looks like:

 

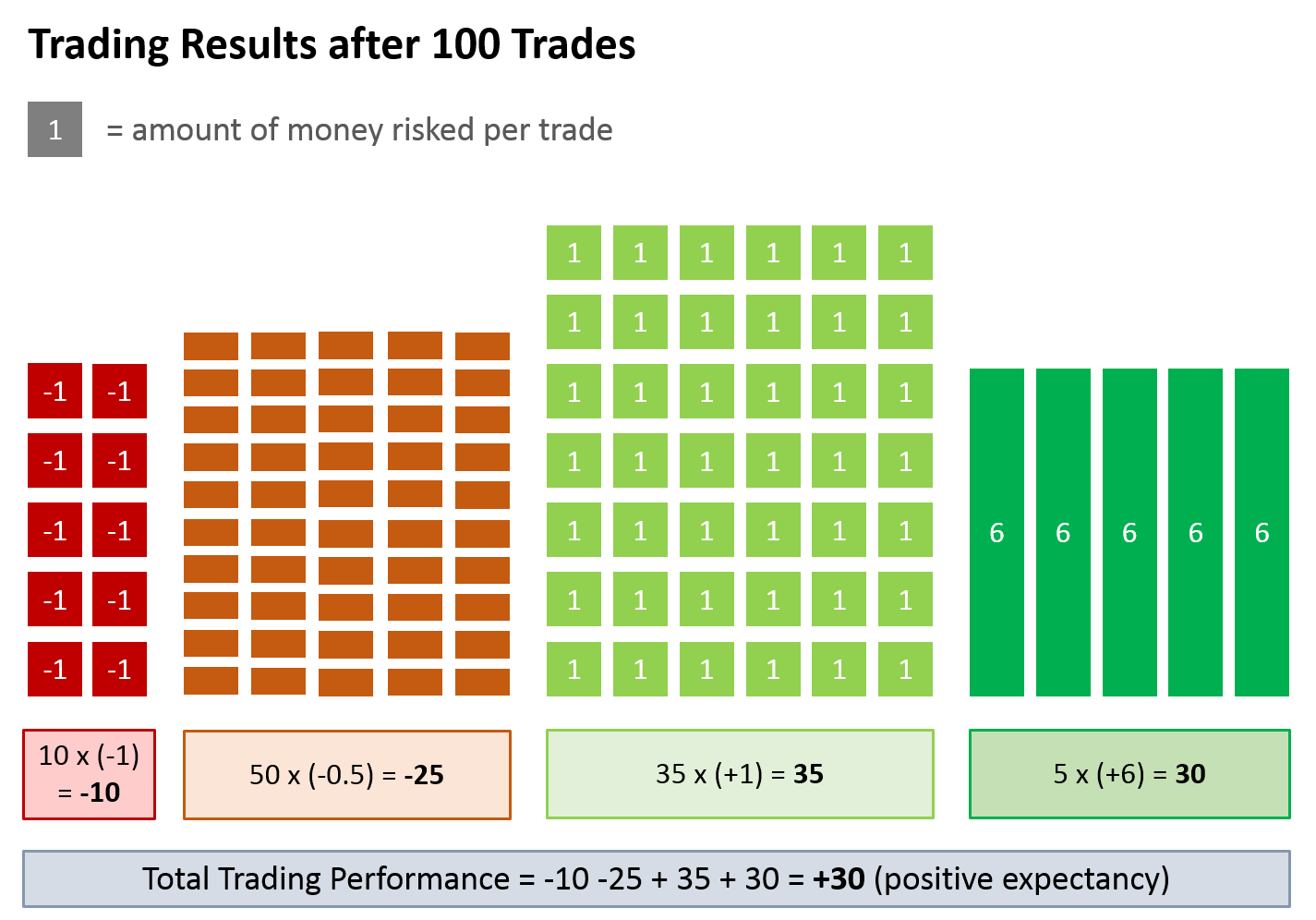
It’s positive expectancy… on average, we would make 30 times the amount we risked for each trade, over 100 trades.

That sounds good… but how would that look like?

I created a simple simulation in a spreadsheet over 100 trades to see how it the portfolio value could develop.

 

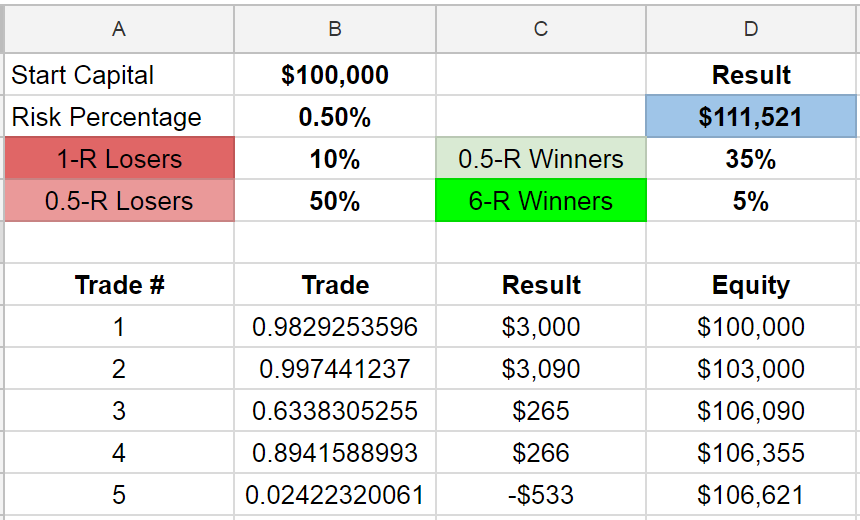
It uses random numbers to create the results that we use as trades and calculates the money in the portfolio after each simulated trade.

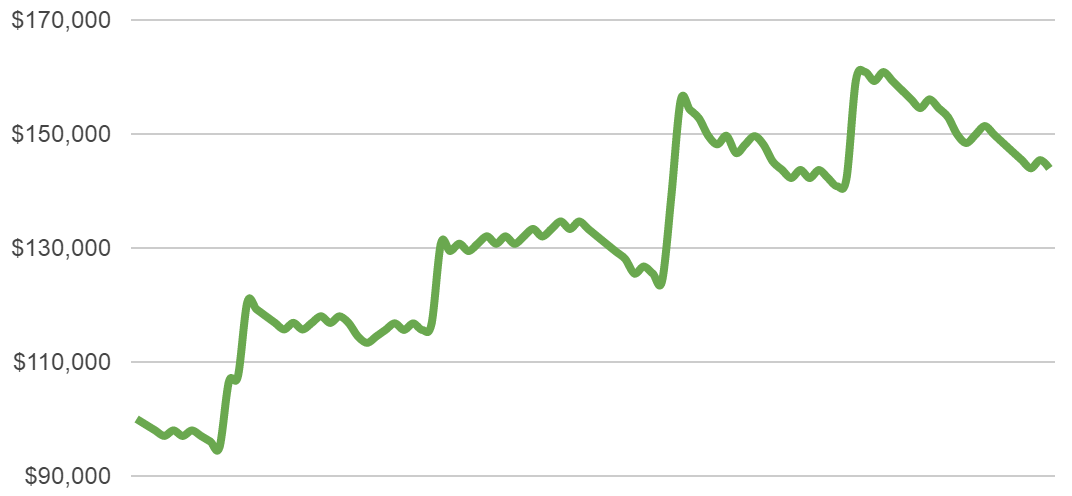
Here is how that looks on a chart over 100 trades:

 

 

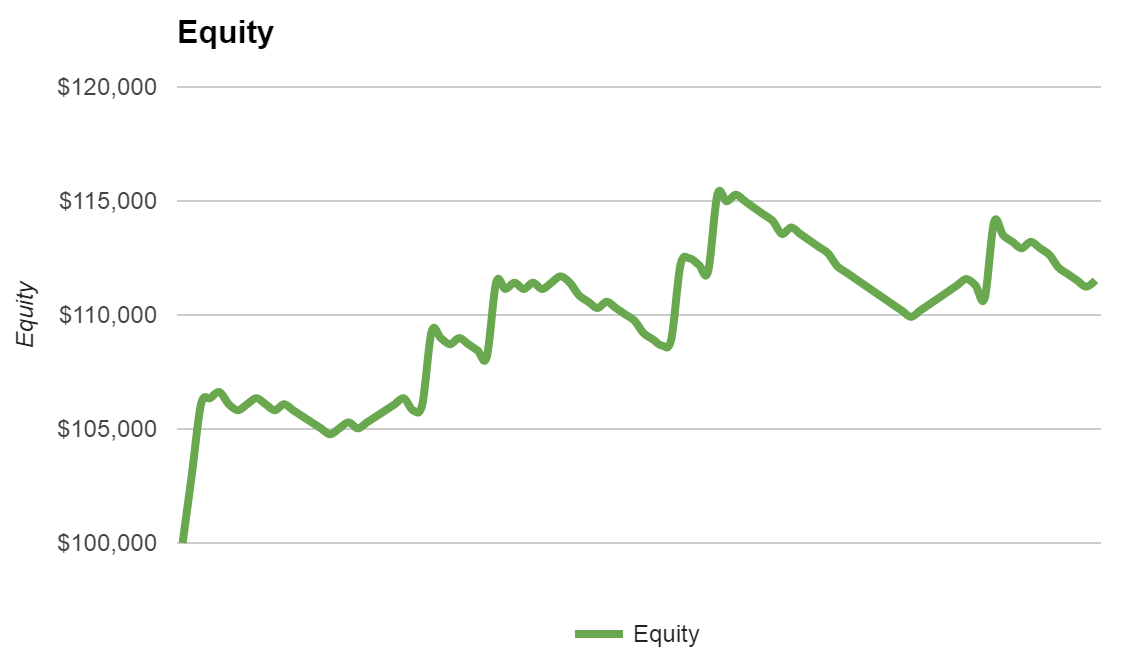
You can see the long streaks of losing trades.

That’s because the probability of having a losing trade is at 60%. It’s psychologically taxing to see gains dwindle away like that. It’s the few big winners that make most of the gains – that’s why it is so important to catch as many opportunities as possible.

This is a simple type of Monte Carlo simulation – simulating possible outcomes.

Because of using random numbers, this simulation should be run many times to see how often each outcome happens. I am not doing this here though – it’s just a quick example.

In practical trading the results vary much more – after all, there are not only 4 types of trade results like we used here for the simulation.

What would happen if we increase the risk per trade?

The chart would look more erratic and the results more extreme. There will be scenarios where fantastic returns are made, and plenty others where we would see bankruptcy loom.

Lower risks per trade will keep these extremes away (they still can happen but it’s less likely).

 

Some more examples with varying risk settings

 

Here are some more examples of how those 100 trades could develop with our 0.5% risk setting:

 

 

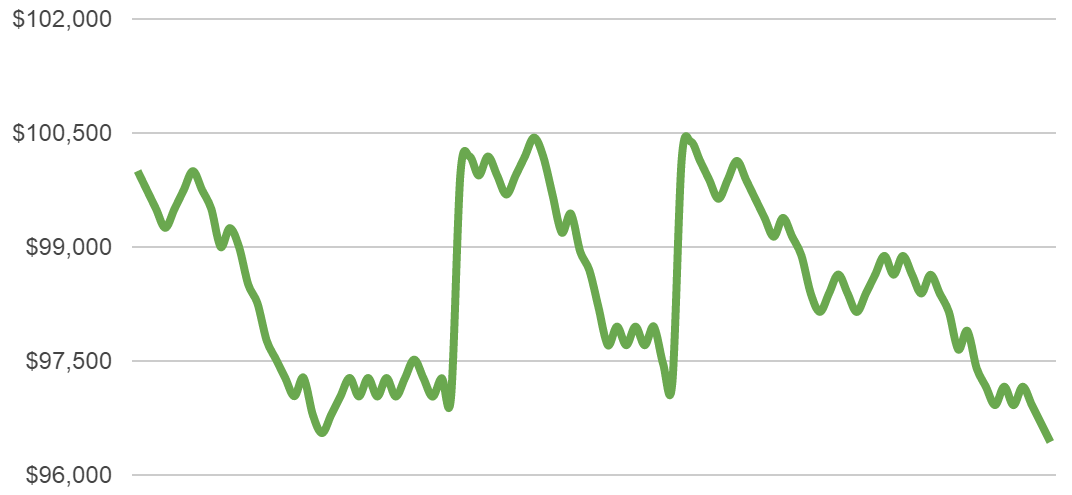
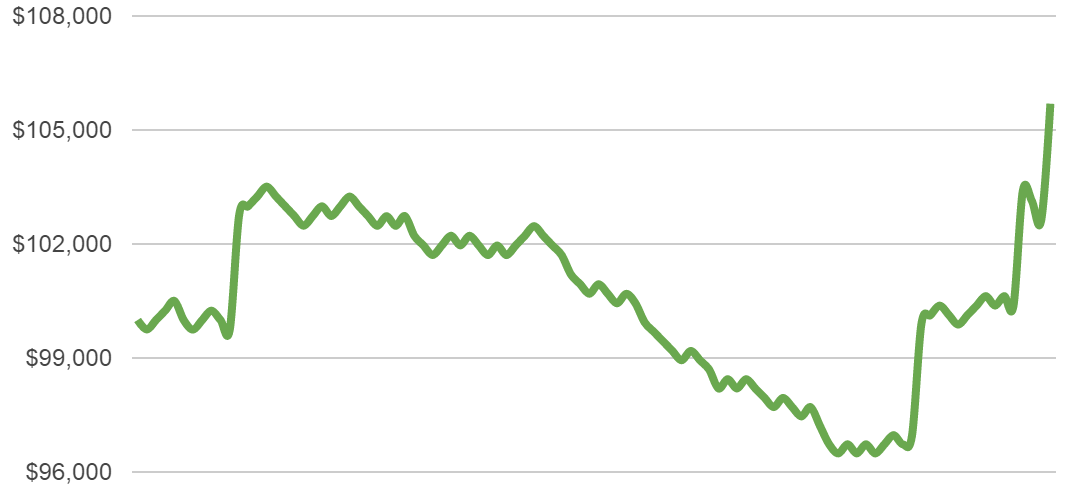
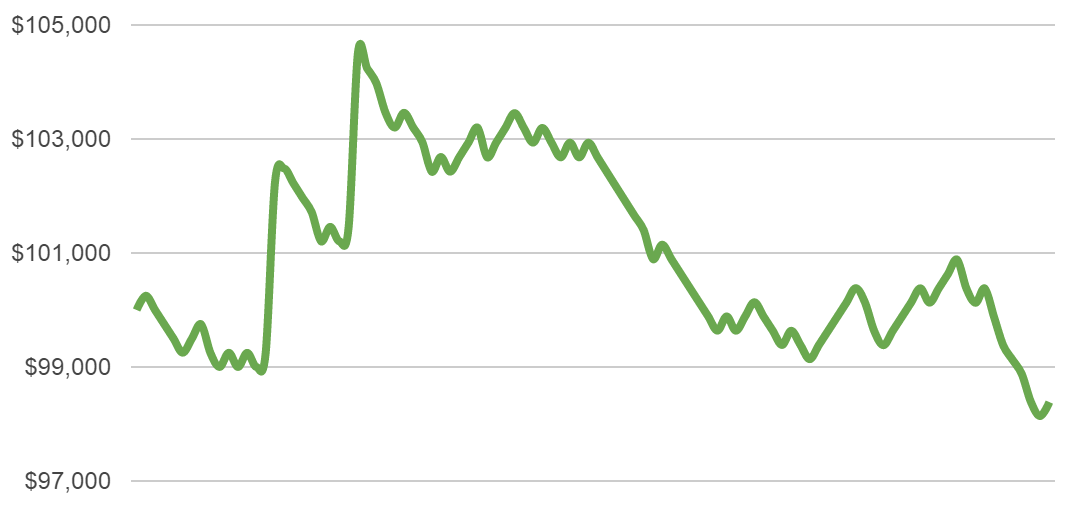
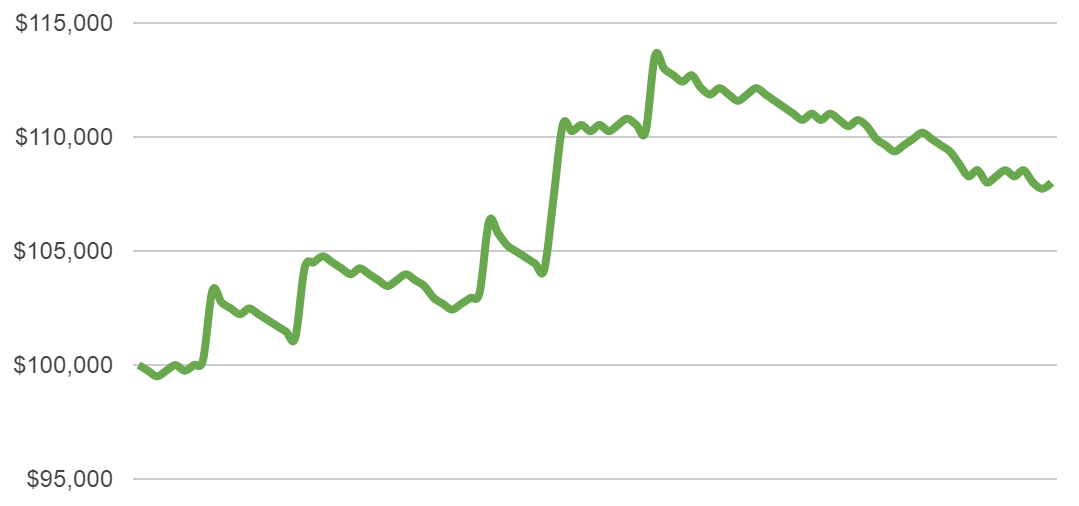
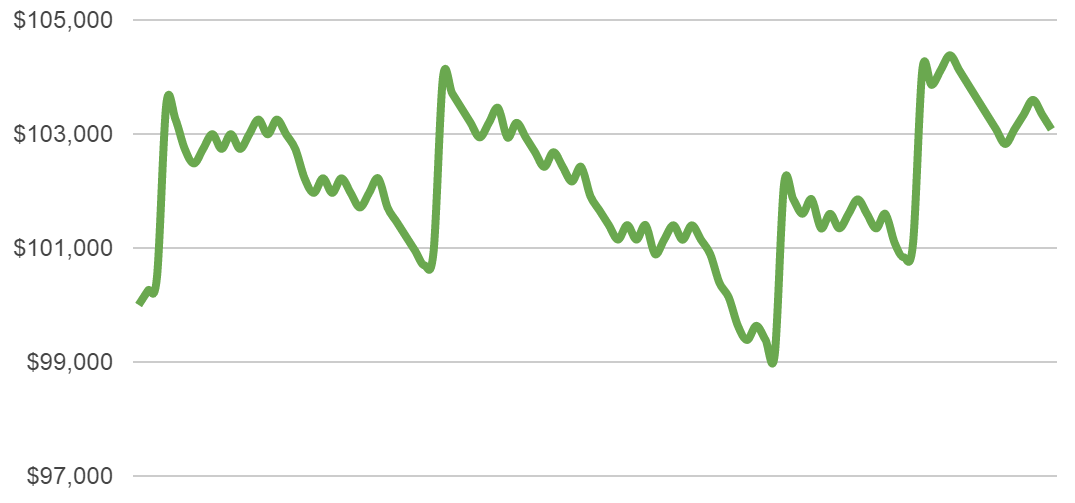
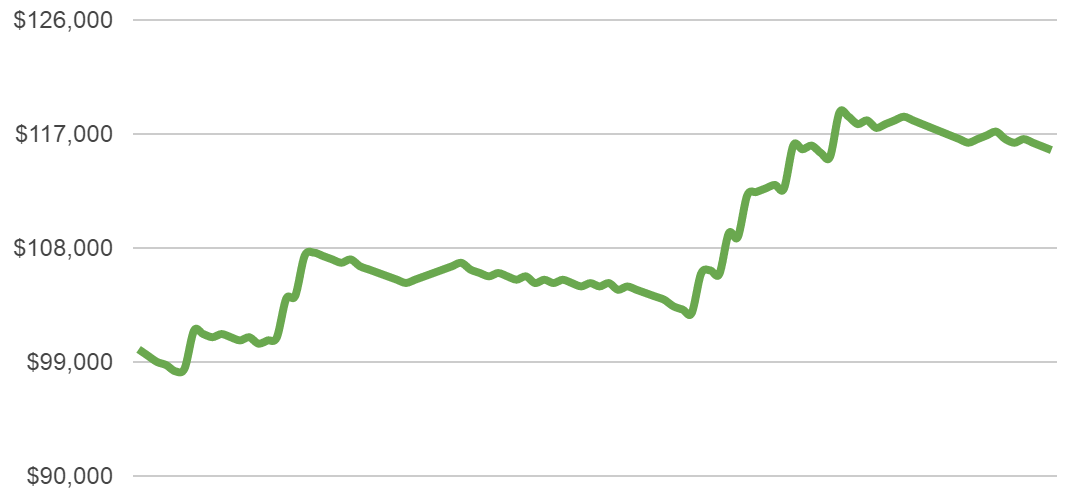
Most scenarios are not too extreme – there are cases with good returns, others are average and some are in the negative. But we are not losing huge amounts of money in any of them.

Now let’s crank up the risk setting to 2% of capital:

 

 

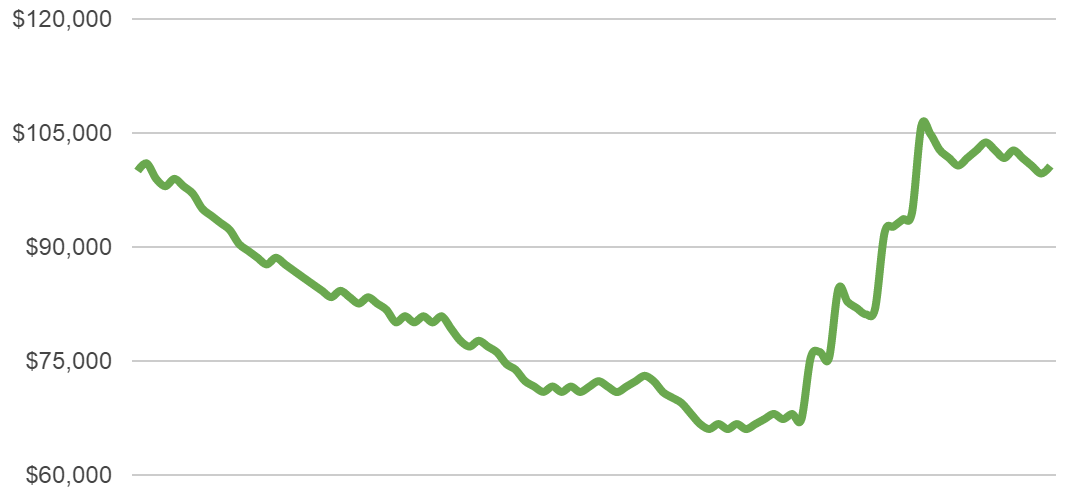
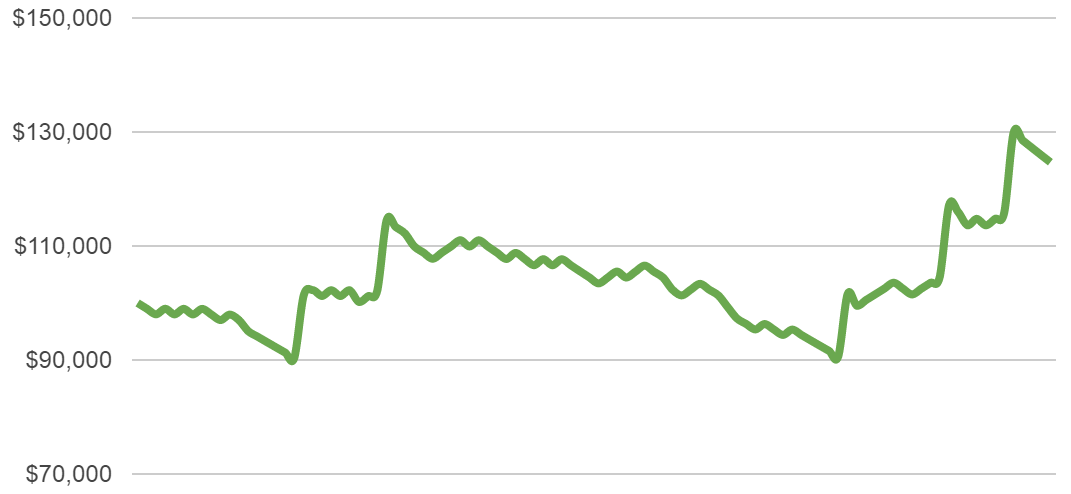
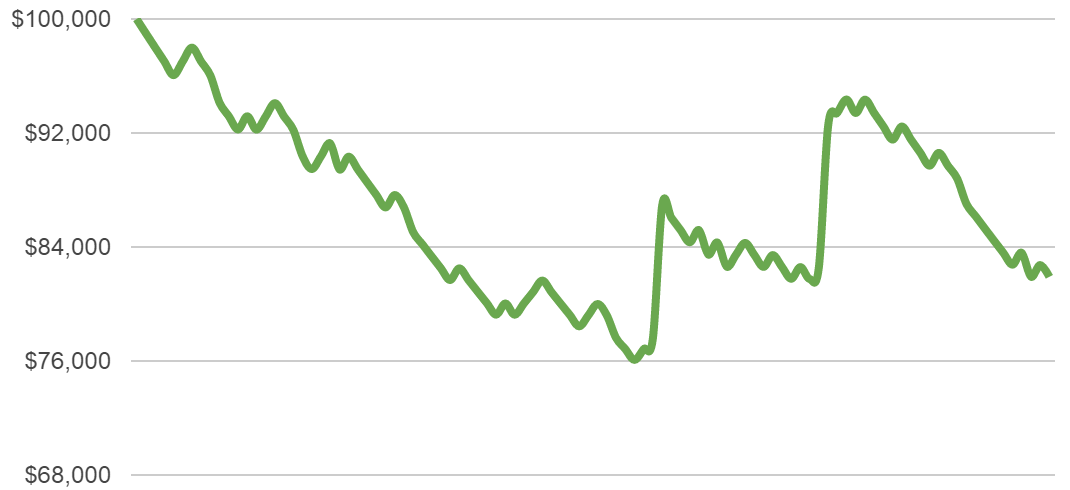
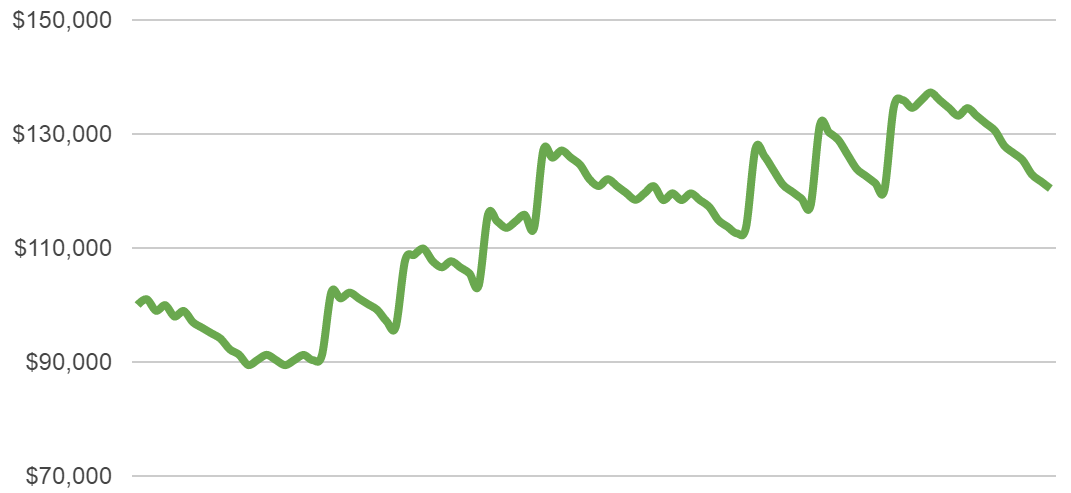
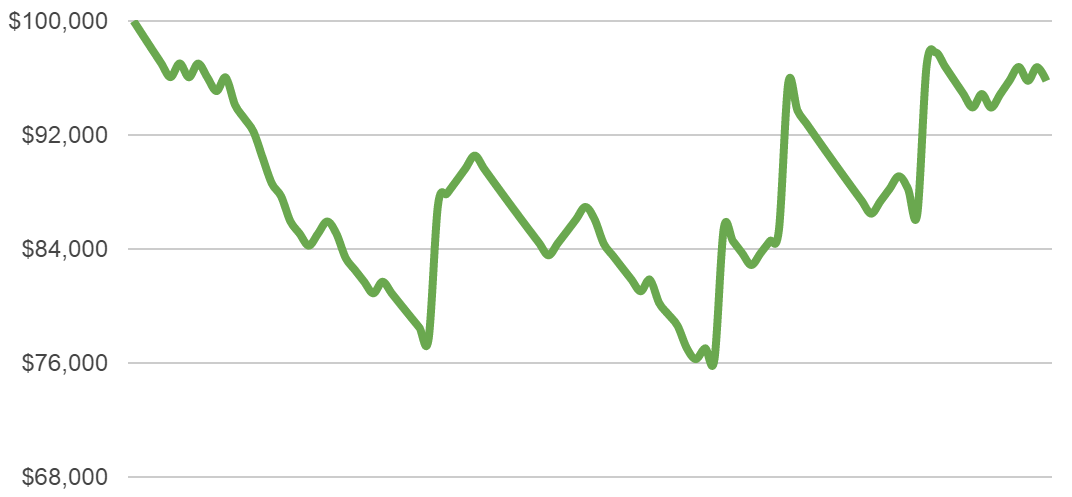
In these cases, the charts are more volatile.

There are far higher gains possible, but also far higher losses. In half the cases the drawdowns go down to 25% of start capital or worse.

Most people would have great difficulties to accept such losses, even if they know that in the long run, they should eventually recover from them (or not – if risk settings are too high).

 

How low could we go with our risk setting?

Is there a lower limit for limiting the amount of money at risk?

How about 0.25%? Or 0.1%? Or even less? How will it affect trading performance?

Will the risk go even lower? Will our gains suffer?

Yes and no… there are practical limitations in both directions. A great way to understand system limitations is to go through a couple of examples that are on the extreme side.

 

1st Example: Risking $50 per trade, with $100,000 capital

I will use the same numbers as Trade #1 earlier, only that the risk setting is at 0.05% or $50 per trade with a total portfolio value of $100,000.

Trade #1 looked like below:

 

 

• Buy Price: $100
• Stop Price: $90, stop difference = $10 per share
• Stocks to buy = $50 / $10 = 5 stocks
• Buying 5 stocks at $100 each will cost us $500

So far so good. Now let’s sell it again after its trend reversal.

• Sell Price: $130
• Total Gain = 5 x ($130 – $100) = $150
• Reward to risk ratio remains the same: 3:1

Now where are the problems?

First, brokerage fees. They vary strongly between brokerages, but let’s say for the sake of the example that the brokerage has a deal: a flat fee of $10 per transaction for up to 5,000 shares.

In this case, we will be charged $20 in fees for our trade – although we only bought and sold 5 shares each time.

 

 

Now you might say well, it’s expensive but then again, $20 from a gain of $150 is not too bad.

You are right… but that’s not your average trade!

The system we simulated earlier had a positive expectancy of 30x the single risk over 100 trades… that’s an average trade return of 0.3 x Risk taken.

And how much would be our average return if we take a risk of $50?

It’s 0.3 x $50 = $15.

But that’s before paying trade fees. And how much is left after paying your $20 per trade?

Less than ZERO! On average, we would lose $5 per trade… sounds like playing roulette in a casino, with the long-term odds against you.

The picture below shows the performance difference for the same trading system, with and without fee payments.

 

 

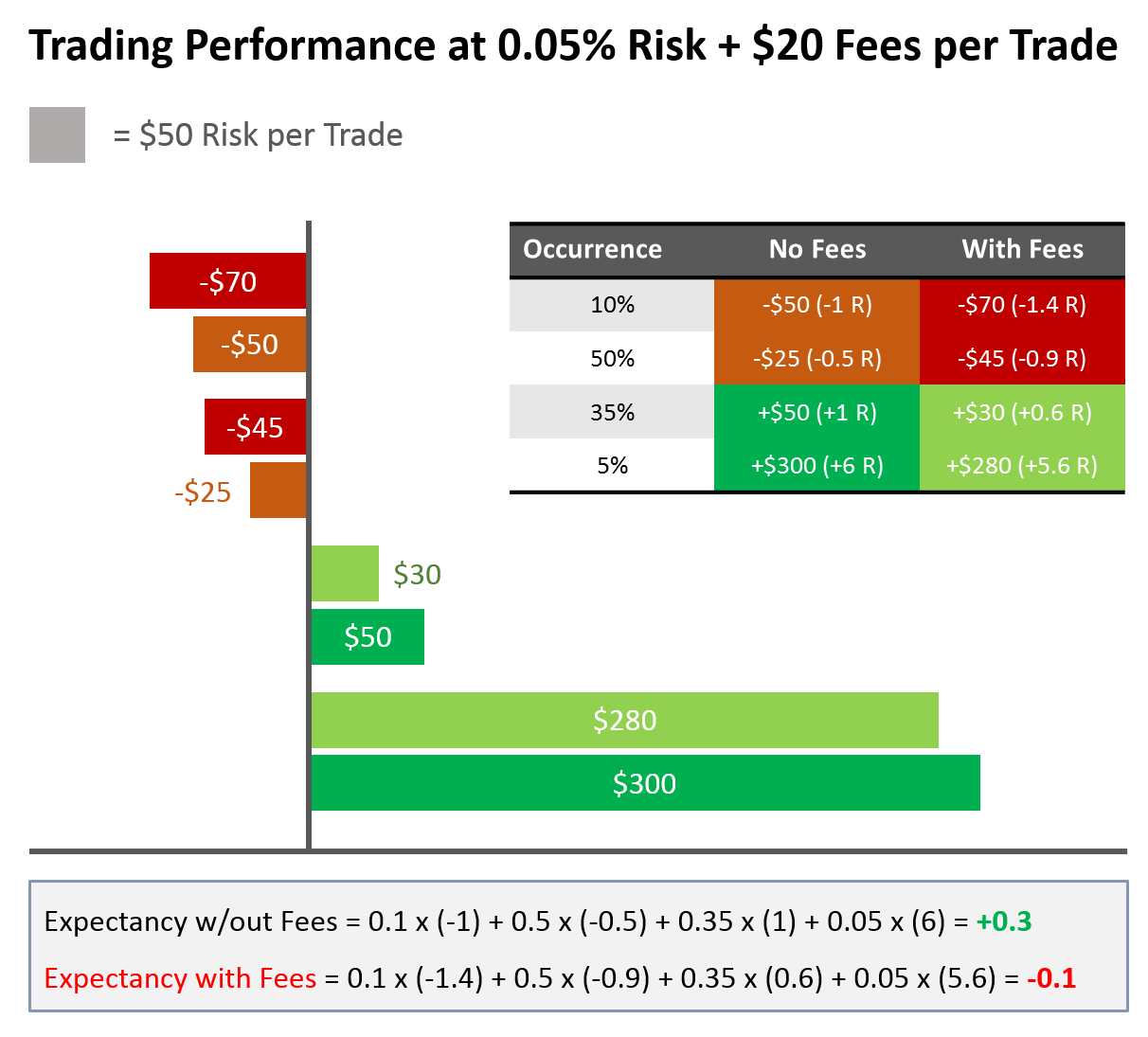
Fees alone turned this system from having a positive expectancy into one with negative expectancy.

That’s really BAD!

How would the system be affected by a risk setting of 0.5%?

The average trade return would be 0.3 x $500 = $150 before fees… and $130 per trade after fees. Still not great, but better than before.

So, reason #1 that speaks against very small risk settings is trading fees.

The smaller your risk per trade, the stronger will fees impact performance.

And what’s reason #2?

Small risks yield small returns (in dollar values) – so to improve your yearly performance, you will need to make more trades.

That not only means more fees in total but also more work. Instead of making one trade you must make now make ten trades. Ten times the time to decide. A longer list to choose from, etc.

At some point, it does not make sense to take smaller risks.

Your potential gains (lower portfolio drawdowns) will be eaten up by fees instead, and you need to spend much more of your precious time with trading.

 

2nd Example: Risking $25,000 per trade, with $100,000 capital

Now let’s look at the opposite case… taking a very large risk of 25%, or ¼ of our capital.

We already know that it’s a risky thing to do… but just for fun, how would such a trade look like?

Here’s the math:

• Buy Price: $100
• Stop Price: $90, stop difference = $10 per share
• Stocks to buy = $25,000 / $10 = 2,500 stocks
• Buying 2,500 stocks at $100 each will cost us $250,000 (oops!)

First, the good news. We will only pay $20 trading fees… quite negligible. Yay!

But now, the bad news. We only have $100,000 in cash… but we need $250,000 to take this trade.

Usually, that means that we cannot exercise such a trade. Which is probably a good thing, because even if we could do it, the chances of going broke are very high.

What else could be the problem?

Imagine we could exercise this trade (we inherited $150,000 from a rich aunt we knew nothing about). Could superior performance justify taking such a risk?

 

 

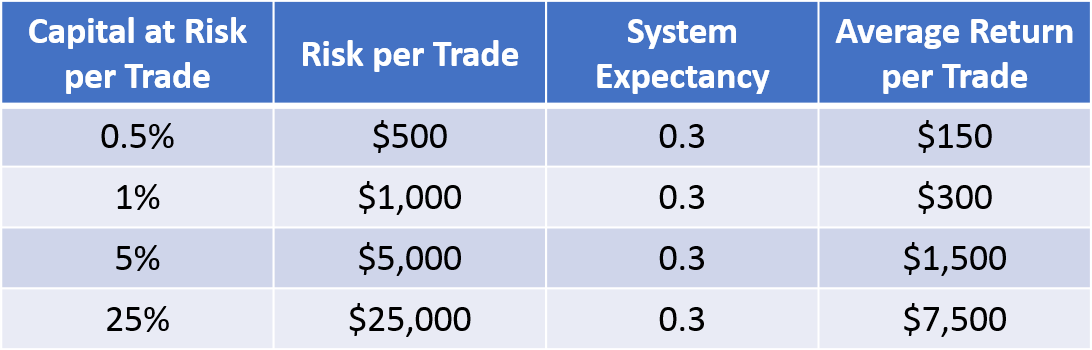
If we forget about the massive risk we are taking by using 25% of our capital (I know it’s less now after the inheritance, but stay with me here), a return of $7,500 looks better than a return of $150…

But we forgot about another critical parameter… the effect of time.

 

The effect of time on investing – it’s not what you think

When we think about time and investing we think about exponential growth… the earlier you start, the better in the long run.

That’s correct, but that’s NOT what I am talking about here.

I am talking about how long we hold on to a trade.

It depends on your trading system type – day traders, as the name implies, hold on to their trades for maximum one day. When trading short term trends, like in band trading, it’s usually no more than a few weeks.

But trading medium to long term trends is a different story.

If the trend develops nicely, we might hold onto these shares for years! And for other trades, the ones that are mediocre, it’s 4 – 12 weeks.

To keep it simple, let’s assume that an average trade means that we will hold on to the shares for 2 months. And each trade binds a part of our capital.

So how many trades can we do per year, depending on our risk setting?

Let’s assume we need 10 times the amount of capital compared to our risked amount (that’s equivalent to a 10% trailing stop, a good baseline value).

 

 

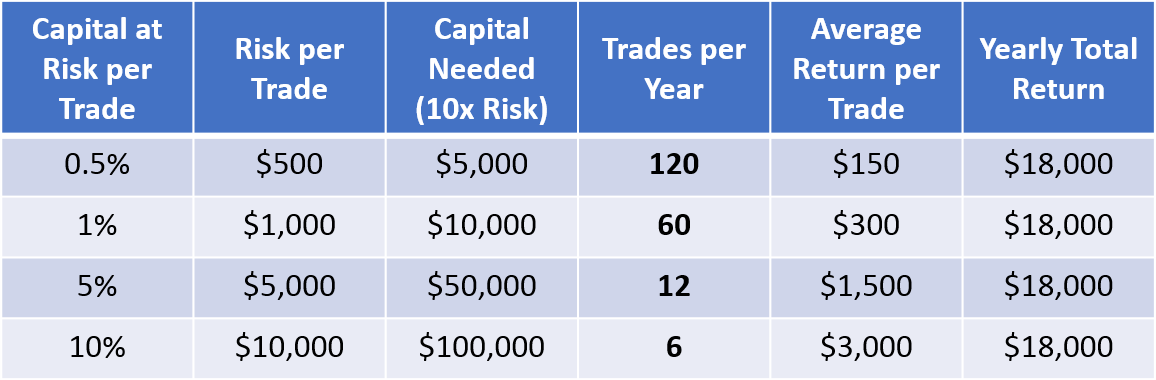
If we trade with a risk setting of 10% of our capital, for each trade all our cash is invested in a single trade.

And with a single trade lasting for 2 months (on average), we can exercise 6 trades per year. With each trade gaining us (again, on average) $3,000, that is a total gain of $18,000 per year.

Not bad.

If we reduce our risk to 1% of our capital, then each trade will bind $10,000 of our capital.

This means we can make 10 trades at the same time. With each lasting 2 months, we can make a total of 60 trades per year. And with each gaining $300, our theoretical yearly return is… also $18,000!

It’s a rough calculation only.

Portfolio value changes over the year, and I used only averages, AND I neglected fees, which is simplistic (to say the least). It’s just a very basic assessment – but it tells a compelling story! It basically says that…

By taking massive risks, you are making – on average 🙂 – no higher gains than with taking small risks.

And for a simple reason – you don’t have the cash to do so.

If you had more money, then your risks would become smaller again – because you would risk a smaller percentage of your total cash.

That’s why I do not like investing in real estate. I would need to risk all my money (or more, if taking a mortgage) for a single trade. It’s like taking a 25% risk with stocks (and the missing $150k would be the mortgage!).

In summary, assuming same results per trade, if you crank up your risk, you are not really improving performance.

You make fewer trades per year, so you pay fewer fees. You could make some great gains, but your chance of large losses will greatly increase.

Next up: some more examples on how to calculate how many stocks to buy, based on real pricing data.

 

Examples based on historical price data

All following examples assume a starting capital of $100,000 and a maximum risk per trade of 0.5% of total equity (equity means cash + money already invested in stocks, i.e. total portfolio value).

 

 

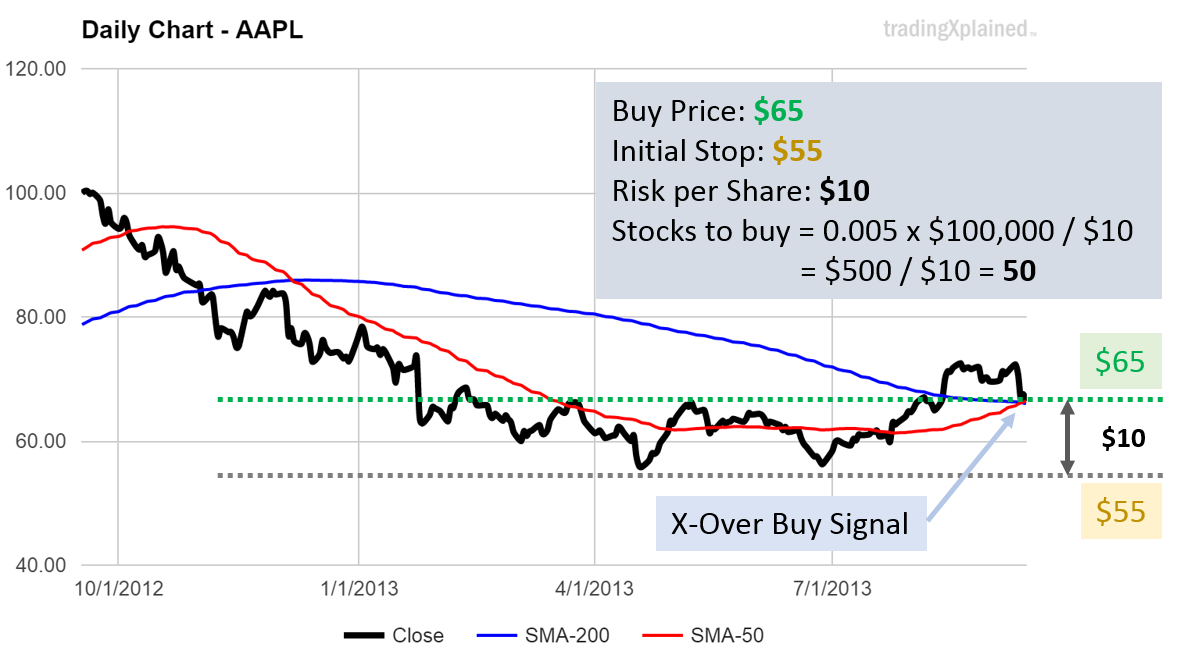
In this chart, we use an X-Over signal to detect a buying opportunity.

The current buy price is at $65 and we put the initial stop price below the lowest prices from the downtrend. That means a risk per share of $10.

With a risk setting of 0.5% of portfolio value of $100,000, we accept a risk of $500 for this trade opportunity.

That means we can buy $500 / $10 = 50 stocks, for a value of 50 x $65 = $3,250.

 

 

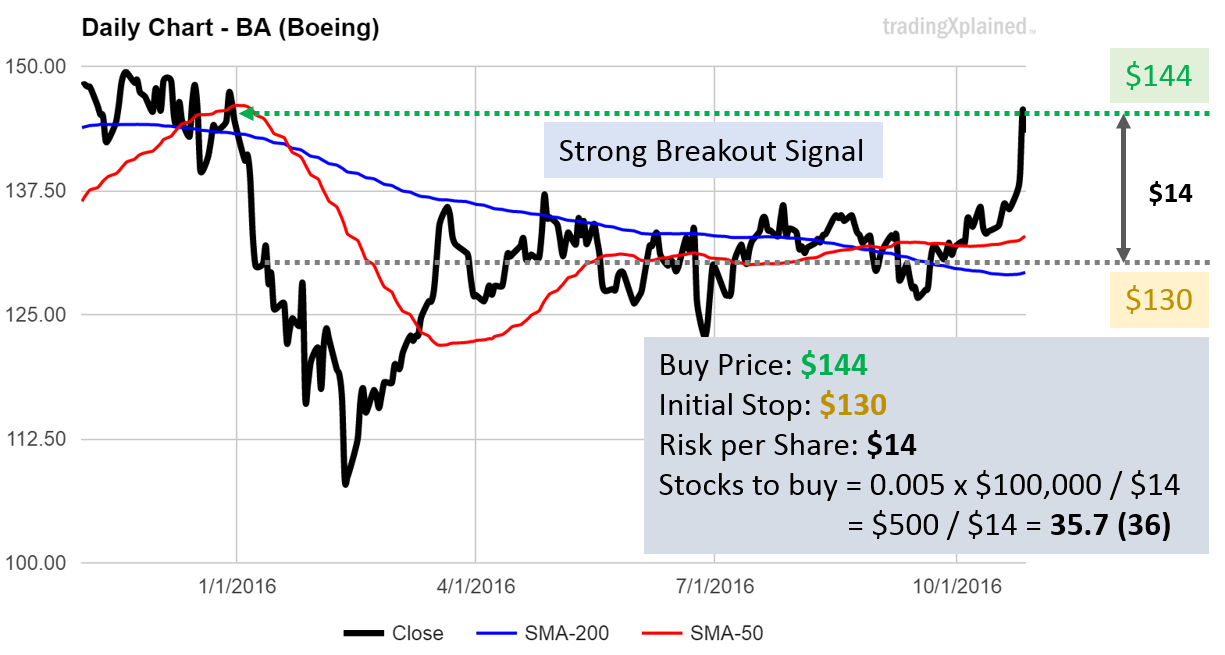
In the above example, we use a breakout signal as buy indicator.

Buy price is at $144, and we set the initial stop at $130 (in the middle of the previous price range, or close to 10% of current price). The assumption is that if prices go to new heights, they are unlikely to go back within the same price range (with a margin of error).

Our trailing stop is $14 (= risk per share), and by again risking $500 for this trade, we can buy $500 / $14 = 35.7 shares.

As we cannot buy partial shares, we round it up to 36 shares. We will spend 36 x $144 = $5,184 on this trade.

 

 

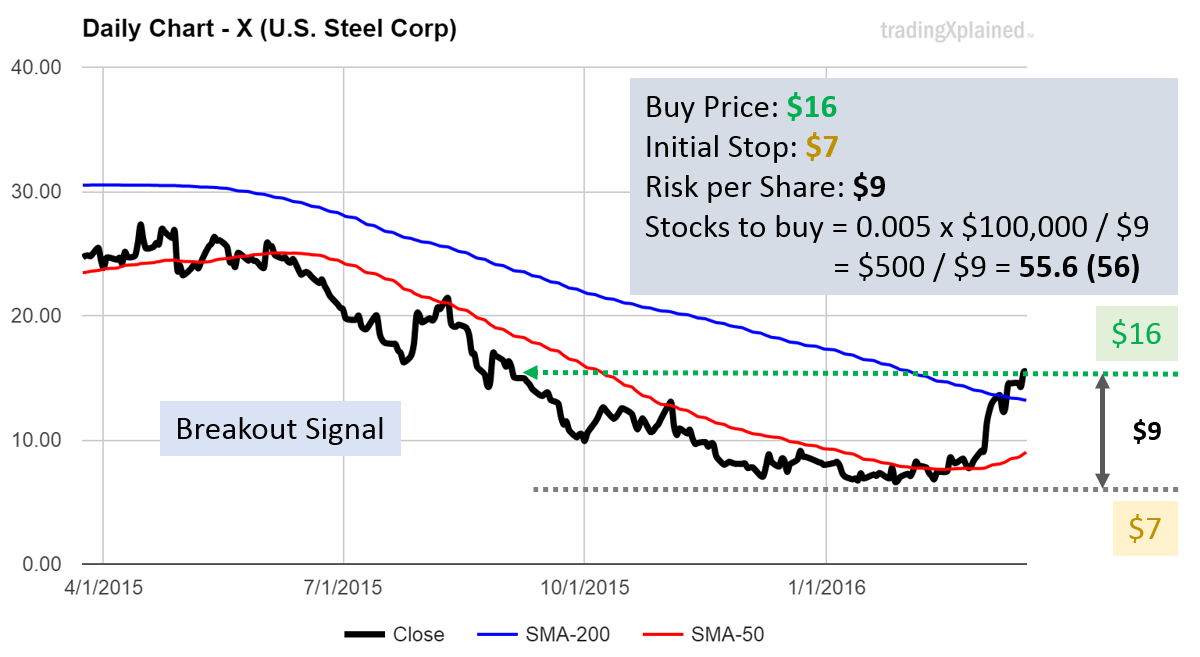
The stock price of U.S. Steel (X) has been falling for over 12 months and might have reached its lowest point.

In the last few months, its value has increased by more than 100%! Our breakout signal indicates a buying opportunity.

Buy price is at $16. A 10% trailing stop would be at $1.60 – but this sudden price rush upwards means that there might be more strong price swings to come. So, I play it safe… and I set the initial stop below the lowest point again.

It’s a massive trailing stop of $9 (more than 50% of the current price).

With a risk of $500 for this trade, we can buy $500 / $9 = 56 shares, at a value of 56 x $16 = $896.

Despite taking the same risk for each trade, the amount we spend on each purchase is very different. That is mainly because we adjust for possible future price swings – we want to continue riding the trend without being bailed out too early.

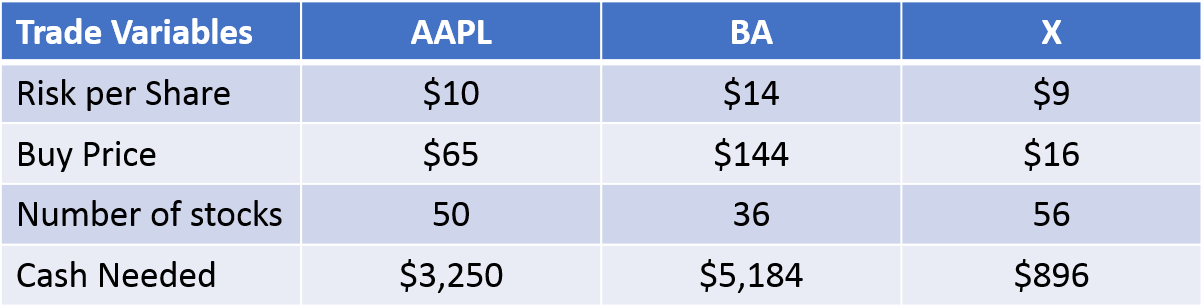
Below is a summary table for the 3 examples above:

 

 

Deciding where to set your initial stop, or your trailing stop takes some experience. After a few trades you will get the hang of it – and if in doubt, stick to the 10% as the first try.

There are ways to automatically calculate the initial stop price, using price volatility as input. However, it is a more complex, advanced topic, which I will cover in a later course.

 

It’s not about gains, it’s about risk reduction

So, now you know how to answer the most important question for each trade: how many stocks to buy?

Update your trading system rules with your risk settings – I suggest you start on the lower side (0.25% is fine, 0.5% is also OK).

In any case, do not go above 2%!

That’s when it gets dangerous and as I showed you already, there is not much to gain by cranking up your risk settings. Instead, your risk of losing money dramatically increases.

Preserving your capital should be your number 1 priority.

This will help you to go through the valley of tears (which inevitably will happen at some point) to be ready when the market is in your favor (or shall we say, in your trading system’s favor).

Get the worksheet to familiarize yourself with more examples and practical tips on how to calculate your stops efficiently, before moving on to the next lesson.

JOIN OUR FREE NEWSLETTER

Get the latest trading techniques right into your inbox.